Misura un grattacielo
Problema
Voglio misurare l'altezza di un grattacielo avendo come dati noti solo la mia altezza
riferimenti storici
storicamente questo problema fu posto nel VI A.C. al matematico Talete di Mileto per misurare l'altezza di una piramide senza poterci salire sopra.
Talete analizzò il problema e , si pose il problema il seguente problema : c'è una proporzionalità tra l'altezza di colui che misura (nota) e l'altezza dell'edificio da misurare (incognita) ?
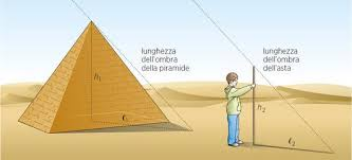
elaborazione strategia : matematizzare il problema
Dalla figura possiamo individuare 4 grandezze che denominiamo :
p = misura altezza edificio (incognita)
px = misura ombra edificio (misurabile da terra quindi nota)
h = misura altezza di colui che misura (misurabile quindi nota)
hx = misura ombra di colui che misura (misurabile da terra quindi nota)
elaborazione strategia : ricercare relazioni per risolvere il problema
Verifichiamo se queste due classi di grandezze sono direttamente proporzionali.
per far questo abbiamo bisogno di entrare nelle ipotesi di un criterio che possa stabilire se queste due classi di grandezze proporzionali
![date un fascio di rette parallele tagliate da due trasversali dal disegno si evince che :
se A[sub]1[/sub]B[sub]1 [/sub]= C[sub]1[/sub]D[sub]1[/sub] [math]\Rightarrow[/math] A[sub]2[/sub]B[sub]2[/sub] = C[sub]2[/sub]D[sub]2
[/sub] cioe i segmenti appartenenti alla trasversale[b] [color=#ff0000]t[sub]1[/sub][/color][/b]e quelli appartenenti alla trasversale [b] t[/b][sub]2 [/sub][color=#0000ff][b]1) conservano l'uguaglianza[/b][/color]](https://stage.geogebra.org/resource/txqrsa2a/XmQsL5e7dY6mhRm7/material-txqrsa2a.png)
![date un fascio di rette parallele tagliate da due trasversali dal disegno si evince che :
se A[sub]1[/sub]B[sub]1 +[/sub] C[sub]1[/sub]D[sub]1[/sub] [math]\Rightarrow[/math] A[sub]2[/sub]B[sub]2[/sub] + C[sub]2[/sub]D[sub]2
[/sub] cioe i segmenti appartenenti alla trasversale[b] [color=#ff0000]t[sub]1[/sub][/color][/b]e quelli appartenenti alla trasversale [b] t[/b][sub]2 [/sub][color=#0000ff][b]1) conservano la somma[/b][/color]](https://stage.geogebra.org/resource/hu4jy6c7/V56XaKv643A2csLv/material-hu4jy6c7.png)
Poichè queste due classi conservano 1) uguaglianza 2) somma allora sono proporzionali
adattare il criterio (teorema di Talete) alla misurazione del nostro edificio
1) consideriamo come rette parallele i raggi del sole
2) consideriamo come segmenti sulla trasversale t1 le ombre dell' edificio px e quella di colui che misura hx
3) consideriamo come segmenti sulla trasversali t2 le effettive altezze : p edificio ed h di colui che misura
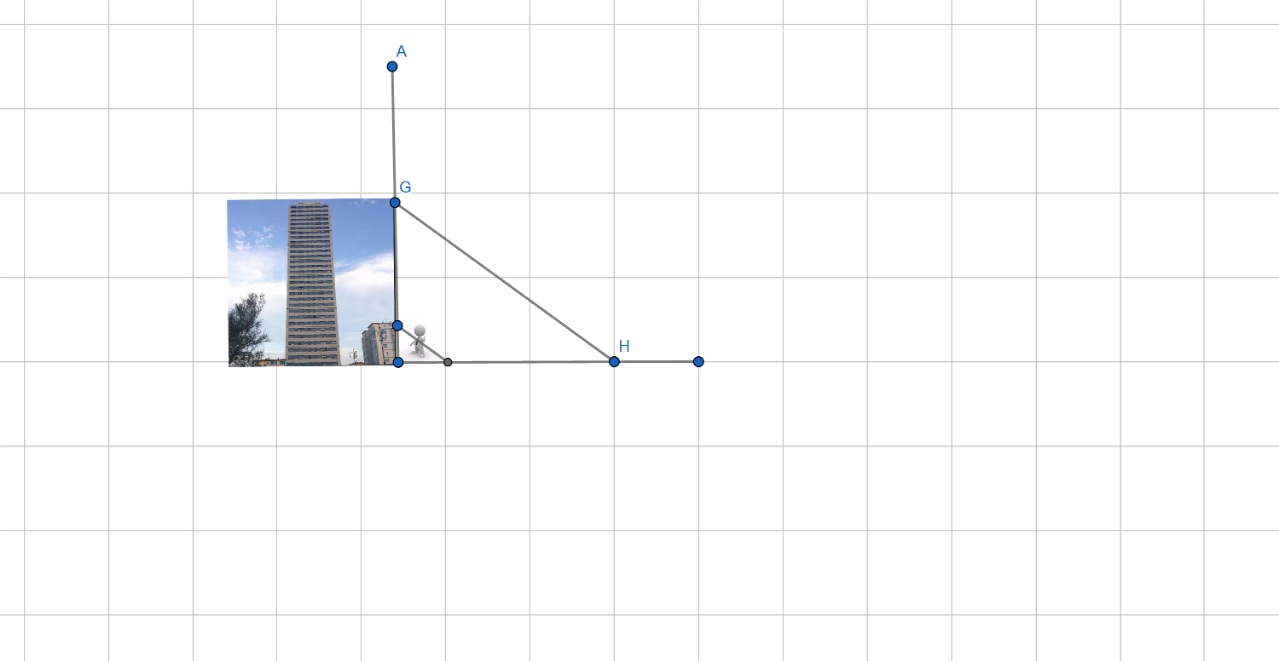
conclusione
applichiamo il teorema di talete:
h : p = hx : px da cui risolvendo la proporzione rispetto a p si ottiene
p = ( h * px )/hx
conclusioni
con l'ultima relazione posso calcolare l'altezza del grattacielo senza nemmeno salirci sopra