Dandelin's spheres
the link between 2D and 3D
You can draw an ellipse using a rope.
In space you can find an ellipse as a cone. But what's the link between both?
In 1822 Germinal Pierre Dandelin proved that both define the same curve.
- In a cone construct two spheres and define the plane tangent to both spheres. The tangent plane defines the known conic (E in the figure).
- Dandelin proved that the tangent points between plane and spheres were the foci F1 of F2 an ellipse equal to the conic E.
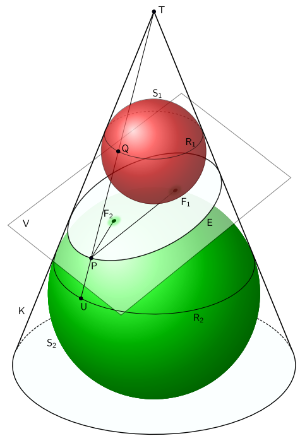
The applet below illustrates the spheres of Dandelin.
- In the construction on the left the incircle and the excircle if a random triangle are drawn. Both circles are tangent to the green edge of the triangle with the two red points as tangent points.
- Drawn in 3D the triangle bcomes a cone and the circles become two spheres Now we see: - the green side of the triangle become an ellipse. - the red tangent points become the foci of this ellipse.