Le relazioni goniometriche fondamentali
LE PRIME RELAZIONI TRA LE GRANDEZZE GONIOMETRICHE
Le grandezze goniometriche sono di fatto la riformulazione di un concetto piuttosto semplice: i lati di due triangoli con gli stessi angoli sono proporzionali tra di loro.
Non si potrebbe risolvere tutto con delle semplici proporzioni, allora?
Evidentemente no. Seno, coseno e tangente collegano questa proprietà dei triangoli con la misura degli angoli che compaiono nel problema e sono una formulazione specifica per capire come cambiando l'angolo cambia la situazione descritta dal problema. La goniometria inoltre approfondisce le proprietà di queste grandezze trovando come sono in relazione tra loro, a volte in modo molto elaborato e complesso. Questo permette ulteriormente di centrare il problema sugli angoli che ne caratterizzano la situazione e risolverlo da questo punto di vista.
Due delle relazioni che legano le grandezze goniometriche sono dette fondamentali, perché sono immediate conseguenze delle definizioni e permettono di comprenderle ancora meglio.
LA PRIMA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA
La prima relazione fondamentale della goniometria afferma che per qualsiasi angolo vale la seguente formula:
Vedremo più avanti che il modo più diretto e semplice per descriverla è considerarla un'applicazione del teorema di Pitagora: essa afferma infatti che seno e coseno di un qualsiasi angolo possono essere considerati come i cateti di un triangolo rettangolo la cui ipotenusa misura sempre .
Fin da subito abbiamo visto che seno e coseno sono legati ai cateti di un triangolo rettangolo, quindi questa relazione appare abbastanza naturale. In seguito daremo nuove definizioni, ovviamente equivalenti, delle grandezze goniometriche e vedremo che da questo nuovo punto di vista questa relazione è addirittura banale. Per il momento otteniamo qui sotto la relazione fondamentale partendo da un triangolo rettangolo qualsiasi e dalle definizioni di seno e coseno.
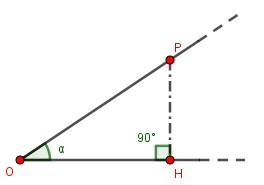
Abbiamo che e , quindi
Il che facendo il denominatore comune, ci porta a:
Dove al numeratore abbiamo applicato il teorema di Pitagora, ottenendo l'ipotenusa che poi si semplifica, riportandoci al risultato atteso.
La prima relazione fondamentale è importante perché ci permette di ottenere il seno a partire dal seno e viceversa. Ad esempio se vogliamo ricavare il seno abbiamo:
isolo il coseno...
applico una radice per eliminare la potenza
Da notare che a partire da un certo valore di otteniamo due valori, opposti tra loro, per . Capiremo meglio il significato di questo doppio risultato con le nuove formulazioni di seno e coseno.
LA SECONDA RELAZIONE FONDAMENTALE DELLA GONIOMETRIA
La seconda relazione fondamentale che si ricava in modo ancora più semplice e mostra che la tangente è pari al rapporto tra seno e coseno:
Abbiamo già ricavato questa relazione nel capitolo precedente; un mono alternativo per ottenerla è considerando che:
Grazie a questa relazione possiamo esprimere la tangente non più basandoci necessariamente sulla definizione e quindi sui cateti di un triangolo, ma utilizzando direttamente le funzioni seno e coseno dello stesso angolo. Da notare che ogni cateto viene sostituito con la funzione ad esso associata - seno per quello opposto e coseno per quello adiacente - quindi la relazione è molto semplice da ricordare.