Der optimale Torschusswinkel ::: Unterricht mit MMS
Kurzinformation
- Einführungsphase Mathematik
- Funktionen und Analysis
- Fußball - Der optimale Torschusswinkel
- Ziel: Numerische Ermittlung von Extremwerten trigonometrischer Funktionen im Anwendungskontetxt
- Dauer: 90-180 Minuten
- Schüler:innenmaterial: https://www.geogebra.org/m/war79au3
- Spezielle Materialien: AB Spielfeld
Vorwissen und Voraussetzungen
Die SchülerInnen können...
- in einem GeoGebra-Arbeitsblatt Dreiecke in ein Koordinatensystem einzeichnen und die Größen berechnen (lassen),
- mit der Tabellenansicht arbeiten und darin Zeilen kopieren,
- mit Hilfe des pythagoräischen Lehrsatzes Dreiecksseiten ermitteln,
- im beliebigen Dreieck Winkel mit Hilfe des Kosinussatzes ermitteln,
- numerisch (mit Hilfe der Tabellenkalkulation) Extermwerte bestimmen.
Lernergebnisse und Kompetenzen
Kompetenzen, die durch den Materialeinsatz aufgebaut werden können:
Die SchülerInnen können...
- die Situation auf dem Fußballfeld durch eine Situation in der Drecksgeometrie modellieren,
- in der Tabellekalkulation systematisch (z.B. durch das Intervallhalbierungsverfahren) den Maximalwert ermitteln,
- Funktionale Abhängigkeiten verschiedener Größen unter Verwendung der Spur- bzw. der Ortslinienfunktion untersuchen,
- verbalisieren, wie man explorativ einen Extremwert bestimmt.
Didaktische Hinweise zur Aufgabe
In einem reichhaltigen Kontext aus der Welt des Fußballs verknüpfen die Lernaktivitäten
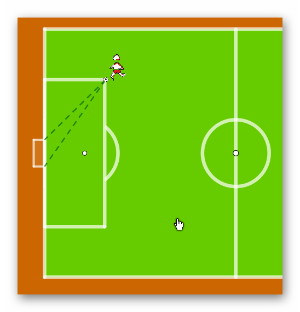
die Themenbereiche „Trigonometrie“ und „Extrempunkte“.Die Trigonometrie liefert die mathematischen Grundlagen zur geometrischen Modellierung der Situation: Der Kosinussatz ist zentral für die Bestimmung des Schusswinkels eines Fußballers in Abhängigkeit der Entfernung zu den beiden Pfosten eines Tors mit bekannter Breite. Darauf aufbauend kann dann untersucht werden, an welcher Position eines Laufweges der Schusswinkel am größten ist. Aufgrund des nichttrivialen trigonometrischen Zusammenhangs, kann das Extremum hier nicht ohne weiteres kalkülhaft über die „Standardmethode“ (notwendiges und hinreichendes Kriterium) gefunden werden. Stattdessen wir ein numerischer Ansatz unter Verwendung einer Tabellenkalkulation durch das Material angelegt. Auf diese Weise wird die Sichtweise „Maximum als höchster Punkt in einer Umgebung“ gestärkt und damit der Aufbau von Grundvorstellungen zu Extrempunkten gefördert, die nicht auf der Differenzialrechnung aufbauen (vgl. Roos, 2020).
Eine Besonderheit des Kontextes ist, dass bei Laufwegen, die nicht auf das Tor zugehen, unmittelbar nach der Position mit dem optimalen Schusswinkel, der Winkel sehr schnell deutlich schlechter wird. Das bedeutet, dass Genauigkeit bei den numerischen Überlegungen zentral ist. Damit unterscheidet sich die Aufgabe von anderen populären Extremwertaufgaben (z.B. die nach oben offene Schachtel, oder die Milchtüte) bei denen die Funktionswerte in einem nennenswerten Bereich um das Maximums nicht wesentlich abfallen.
Darüber hinaus leistet die Aufgabe einen Beitrag zum Aufbau von Werkzeugkompetenz. Im Fokus liegen dabei neben der Umsetzung der Situation im MMS, die Durchführung numerischer Iterationen mit Hilfe einer Tabellenkalkulation und die Arbeit mit Spur und Ortslinienfunktion.
Veränderungsvorschläge / Zusätze im Material
- Weitere Variationen in der Grundaufgabe
- Umformulierung der Aufgaben
- Erweiterung für die Starken
- Verbindung mit dem Bereich der Analytischen Geometrie
Aktivität 1 | Torschusswinkel messen (10 min + x)
Zum Einstieg soll der Torschusswinkel mit dem Geodreieck ermittelt werden.
AB Spielfeld (10 min)
Umsetzung mit Geogebra (Zeitaufwand variiert je nach Vorerfahrungen)
Link zum Material: https://www.geogebra.org/m/zeya2zvd
Im Sinne des Aufbaus von Werkzeugkompetenz erstellen die Lernenden erstellen die Lernenden anschließend die Situation in einer GeoGebra-Datei.
Aktivität 2 | Der Torschusswinkel beim Freistoß und beim Elfmeter (15 min)
Link zum Material: https://www.geogebra.org/m/efhysgdx
In dieser Aktivität sollen die Lernenden den Torschusswinkel aus zwei speziellen Positionen berechnen.
Dafür erkennen sie, dass
- Berechnungen an einem Dreieck erforderlich sind,
- die zwei unbekannten Seiten mit Hilfe des pythagoräischen Lehrsatzes ermittelt werden können,
- der gesuchte Winkel mit Hilfe des Kosinussatzes berechnet werden kann.
Aktivität 3 | Torschüsse aus beliebiger Position (20 min)
Link zum Material: https://www.geogebra.org/m/gz8zwy9e
In dieser Aktivität sollen die Lernenden den Torschusswinkel aus beliebigen Positionen untersuchen. Mit Hilfe der Tabellenkalkulation soll der maximale Winkel für verschiedene Positionen ermittelt werden.
Aktivität 4 | Diagonale Laufwege (25 min)
A | Link zum Material: https://www.geogebra.org/m/jqarwfbt
Im Sinne des Aufbaus von Werkzeugkompetenz erstellen die Lernenden selbst ein Applet, mit dem sie auch schräge Laufwege untersuchen können.
B | Link zum Material: https://www.geogebra.org/m/vg2tt3sx
Hier arbeiten die Schüler:innen wieder an einem fertigen Applet und untersuchen die Veränderung der Torschusswinkels bei einem beliebigen geraden Laufweg.
Aktivität 5 | Lösung mit Hilfe der CAS-App (optional)
Link zum Material: https://www.geogebra.org/m/yc3bdfpt
Um verschiedene Lösungswege vergleichen zu können, lohnt sich der Blick auf eine Lösung der Aufgabe mit Hilfe eines CAS.
Sicherung / Hausaufgabe / Überprüfen des Lernerfolges
A | Link zum Material:
Wann sollte ein Torwart dem Stürmer, der mittig alleine auf ihn zuläuft, entgegenstürzen?
B | Link zum Material: https://www.geogebra.org/m/mwnfx6kg
Wo ist der Ort für einen Spieler, für den die Summe der Abstände zu drei Mitspielern minimal ist?
Probleme und Lösungsmöglichkeiten
Diese Aufgabe kann eingesetzt werden bevor die Schüler:innen das "Standardverfahren" (erste Ableitung gleich Null setzen, mit der zweiten Ableitung prüfen) für die Ermittlung von Extremstellen kennengelernt
haben oder im Anschluss daran. Im ersten Fall hilft der Zugang dabei, eine inhaltliche Vorstellung von lokalen Extrema aufzubauen, auf die später Bezug genommen werden kann. Im zweiten Fall wird deutlich gemacht, dass "Standardverfahren" zwar ein mächtiges Werkzeug, aber nicht der einzige Weg zu lokalen Extrema darstellt (Befreiung aus dem Gefängnis des Kalkülhaften). Sie fordert dann die Kreativität der Lernenden heraus, weil die "Standardmethode" sich hier als sehr sperrig erweist und der Wert einer numerischen Lösung im Unterricht hervorgehoben und diskutiert werden kann.
Im Vergleich zu der Untersuchung von die EF dominierenden ganzrationalen Funktionen kann der hier angebotene Zugang Schwierigkeiten mit sich bringen, weil Extremwertsuche im Zusammenhang der Trigonometrie ungewohnt ist und weil das benötigte Vorwissen (insbesondere die Anwendung des Kosinussatzes) nicht unbedingt vorausgesetzt werden kann.
Literaturangaben / Quellen
- Roos, A. K. (2020). Mathematisches Begriffsverständnis im Übergang Schule–Universität: Verständnisschwierigkeiten von Mathematik an der Hochschule am Beispiel des Extrempunktbegriffs. Springer-Verlag.
- Ulla Schmidt: ?