₅Point Location estimators: Geometric Medians on a sphere

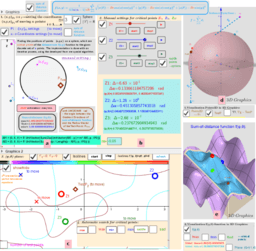
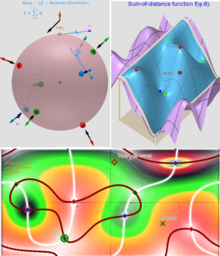
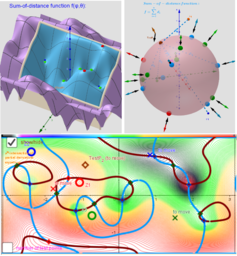
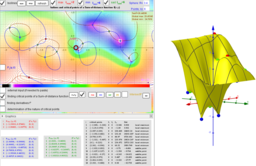
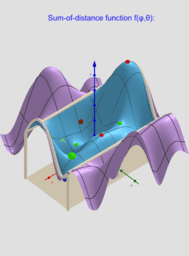
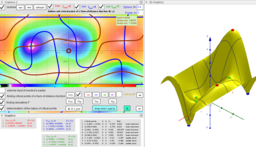
ΛM -Lagrange Multipliers with One Constraint. Finding Estimators of location on a surface of the sphere as Critical points of the corresponding Lagrangian for a discrete set of points. Expanded definition of the Geometric Median https://en.wikipedia.org/wiki/Geometric_median as a point located in a restricted area and which not only minimizes, but also maximizes or is a saddle point for the sum-of-distance function is. Let lP={P1,P2,...,Pn} -set of n points, {(xi,yi,zi)∈ℝ³: i = 1,...,n} -their coordinates is. The Geometric Medians on a bounded area (e.g. sphere S) are defined as points GM on this surface from where the distance sum function of all Euclidean distances to the Pi's are critical points: local minimums, maximums or saddle points. Critical points can be found using Lagrange multipliersas finding the Extreme values of the function f(x,y,z) subject to a constraining equation g(x,y,z)=x²+y²+z²-R². There is a system of equations: ∇f(x,y,z)= λ∇g(x,y,z). A local optimum occurs when ∇f(x,y,z) and ∇g(x,y,z) are parallel, and so ∇f is some multiple of ∇g. *From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp