Three-parameter model transformations of the Octahedron. Extreme distributions.
Three parameters are used to transform Icosahedron faces:
t - for truncating,
q-similarity transformations,
α-angle rotation of faces.
With these parameters, using the well-known Expansion and Snub operations applied to a polyhedron, you can explore various polyhedra and get a number of Archimedean Solids.
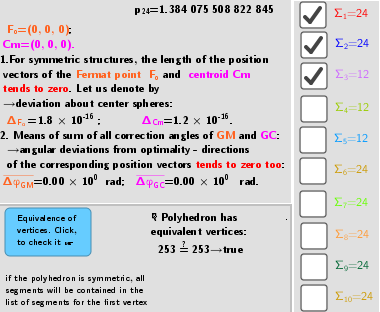
The p (distance sum) is defined here as the ratio of the sum of all pairwise distances between the vertices of the polyhedron to the number of these pairs and the radius of circumscribed sphere. Value p can be given the meaning of the mean distance between the vertices of a polyhedron on a unit sphere.
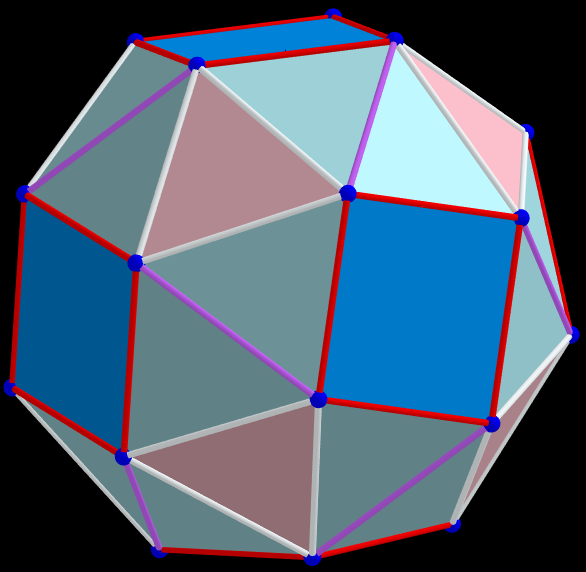
There are three parameters, that are used for three maximizations of the average distance between vertexes. Cases: 8 -corresponds to the Biscribed Truncated Cuboctahedron, 9 -?, 11 -corresponds to the Biscribed Snub Cube.
Values of parameters in the polyhedron model defining the well-known polyhedra.
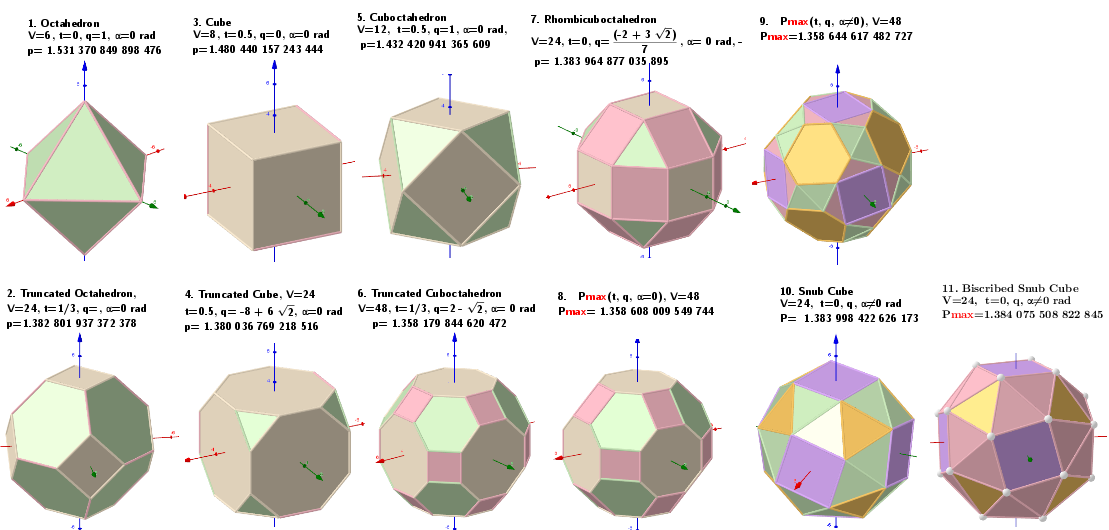
Example 8. Pmax=1. 1.358 608 009 549 744 , t, q, α=0, V=48
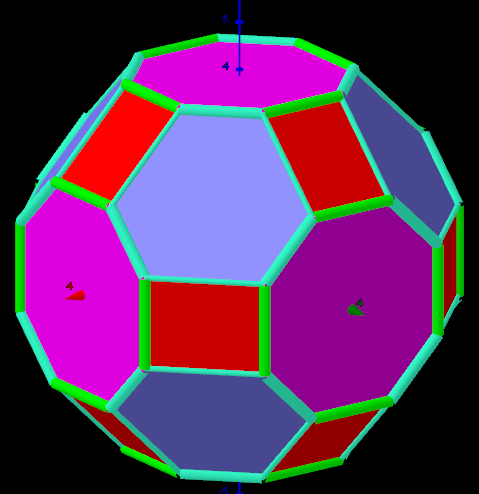


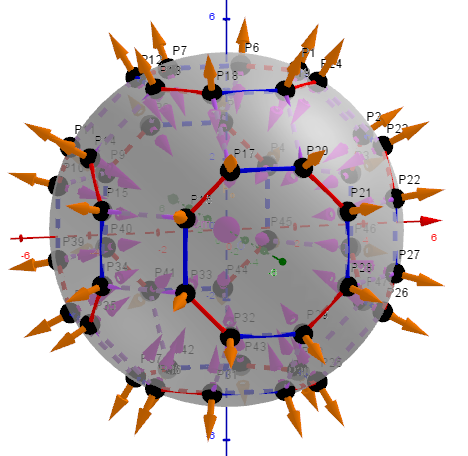
Example 9. Pmax= 1.358 644 617 482 728 , t, q, α≠0, V=120
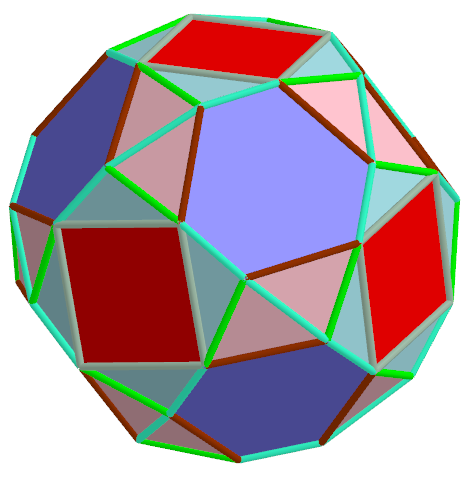


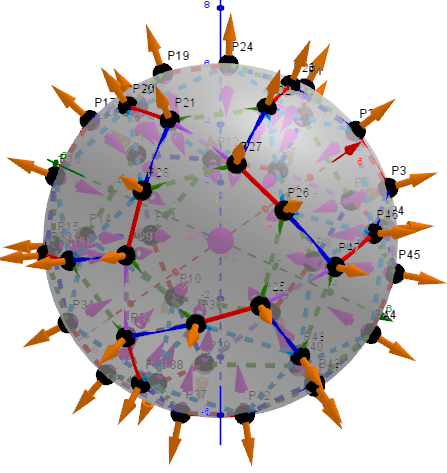
Example 11. pmax =1.384 075 508 822 845; t=0.5, q, α, Biscribed Snub Cube(laevo), V=24.