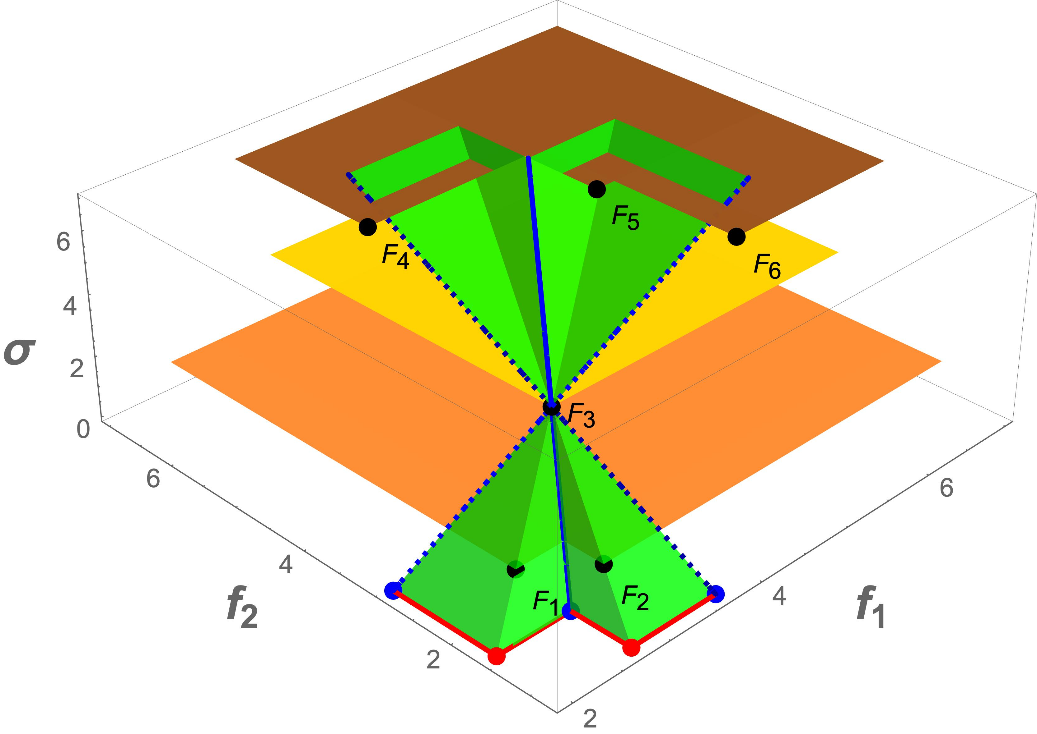
Simple example with Six Points
Potential Pareto Optimality for six hyperintervals on three different $\sigma$-levels.
For most of the values of $\alpha$, $F_3^A$ is dominated by one of $F_1^A$, $F_2^A$, $F_4^A$,$F_5^A$, $F_6^A$. Nevertheless, there is a small neighborhood of $(\alpha_1,\alpha_2)=(0.36,0.53)$ where $F_2^A$ is non dominated.
Figure 7 in "On the Extension of the DIRECT Algorithm to Multiple Objectives" by A. Lovison and K. Miettinen