Thalész tétele
| Tétel: Ha egy kör átmérőjének két végpontját összekötjük a kör bármely más pontjával, akkor derékszögű háromszöget kapunk. |
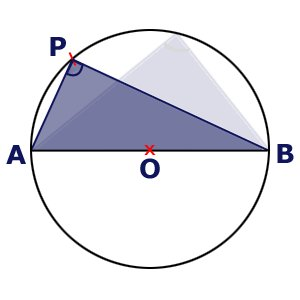
Bizonyítás:
Kössük össze a kör AB átmérőjének két végpontját a körvonal egy tetszőleges C pontjával. Így egy ABC háromszöget kaptunk. Az A csúcsnál lévő CABÐ=a, és ABCÐ=ßA C pontot most kössük össze a kör O középpontjával. Az OC szakasz két háromszögre bontja az eredeti háromszöget.
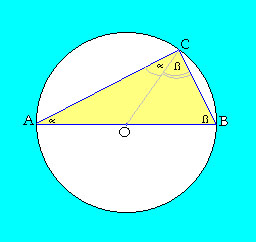
Mindkét háromszög egyenlőszárú, hiszen AO=OC=OB=rEbből következik, hogy ACOÐ=CABÐ=a, ugyanígy BCOÐ=ABCÐ= ß .Az ABC háromszög belső szögeinek összege:
a +b +(a+b)=180° => 2(a+b)=180°, tehát: alfa+béta=90°
Ezzel beláttuk, hogy az ABC háromszögben a C csúcsnál derékszög van.
A tétel megfordítása:
Ha egy AB szakasz valamely C pontból derékszögben látszik, akkor az AB átmérőjű körnek egyik pontja a C pont.Ezt úgy is fogalmazhatjuk, hogy:A derékszögű háromszög köré írt kör középpontja az átfogó felezőpontja. Az átfogó a kör átmérője.
Bizonyítás:
| Tekintsük az ABC derékszögű háromszöget, melynek átmérője az AB oldal, tehát ACBÐ =90° Tükrözzük ezt a háromszöget az AB átfogó F felezési pontjára. C pont tükörképét C' ponttal jelöltük a mellékelt ábrán. A középpontos tükrözés tulajdonságai miatt az így kapott síkidom téglalap, amelynek átlói egyenlő hosszúak és felezik egymást. |
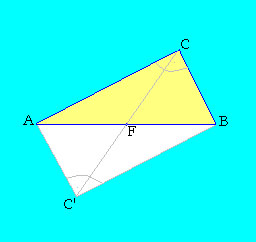
A téglalap F középpontja egyenlő távol van az ABC háromszög mindhárom csúcsától, ezért ez az F pont éppen az ABC háromszög köré írt körének a középpontja, AF=FB=FC a köré írt kör sugara
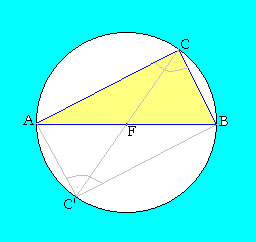
A két állítás egybe is fogható:
Tétel:
A síkon azoknak a pontoknak a halmaza, amelyekből egy adott AB szakasz derékszög alatt látszik, az AB átmérőjű kör, kivéve az AB szakasz két végpontját.
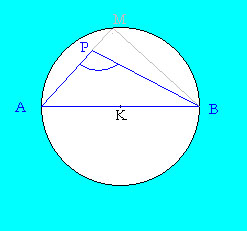
Ha a P pont nem a kör kerületén, hanem a kör belsejében van, akkor a P pontból az AB szakasz tompaszög alatt látszik.
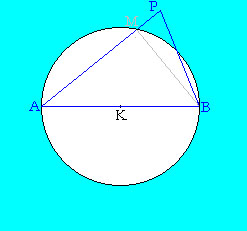
Ha a P pont nem a kör kerületén, hanem a körön kívül helyezkedik el, akkor a P pontból az AB szakasz hegyesszög alatt látszik.
Thalész tétele tekinthető a kerületi és középponti szögek tétele speciális esetének.