Grundlagen Abbildungen Matrizen Basiswechsel
Notationen
ist Basis eines Vektorraumes.
{b1,b2,b3} spaltenweise zu einer Matrix angeordnete Basisvektoren der Ausgangsbasis B.
beschreibt eine Basiswechselmatrix von B in die Standardbasis E={e1,e2,e3}={(1,0,0),(0,1,0),(0,0,1)}T,
beschreibt eine Basiswechselmatrix von der Standardbasis E nach B.
Allgemeine Schreibweisen: nachMatrixvon oder Matrix auch Matrixvon,nach usw...
Ich bevorzuge die erste Version, weil beim Schreiben von aufeinanderfolgenden Basiswechselmatrizen deutlich wird welche Basisversionen aufeinandertreffen und ich kontrollieren kann ob die Basisvektoren auch zusammenpassen! z.B.:
Eine Basiswechselmatrix von B nach B' würde dann heißen und durch zwei zusammengesetzte
Abbildungsmatrizen beschrieben werden können:
- von B nach E und von E nach B'
- Aufsammeln der Basisvektoren =B={b1,b2,b3}, =B'={b1',b2',b3'}
- und invertieren der Ziel-Basiswechselmatrix B'
(1)
Allgemeines Grundprinzip:
Sei B={b1,b2,..,bn} Basis eines Vektorraumes in Koordinaten der Einheitsbasis und V={v1,v2,..,vn}_B Vektoren in B-Koordinaten dann stellt V die Wechselmatrix V->B dar V= bTv .
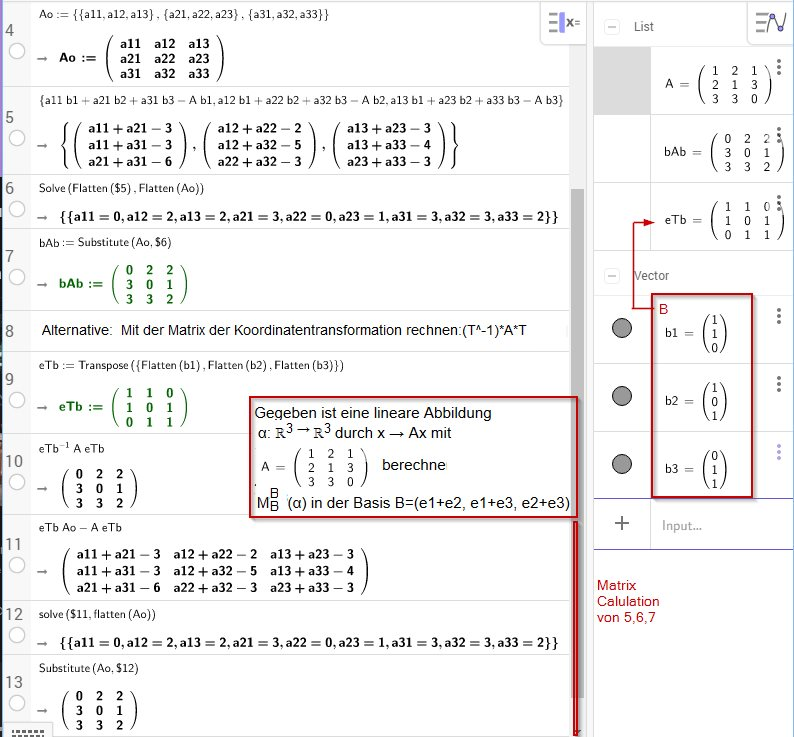
 | ggb-Hinweis: Falls B aus Vektoren besteht muss eine Wandlung in eine Liste erfolgen um damit Matrizen spaltenweise zusammensetzen zu können b1=(1,1,0) b2=(1,0,1) b3=(0,1,1):
eTb:=Transpose({Flatten(b1),Flatten(b2),Flatten(b3)})
eTb:=Transpose(Identity(3) {b1,b2,b3})
Erstellt die Matrix aus den Basisvektoren. |
Die einer linearen Abbildung f zugeordnete Matrix A kann grundsätzlich durch Abbildung der
Basisvektoren erzeugt werden.
Soll f in einer anderen Basis C={c1,c2,c3} beschrieben werden, als cfc, dann müssen für die
Abbildungsmatrix cAc
- die C Basisvektoren abgebildet werden
- die dann mit den Koordinaten der C Basis beschrieben werden
 | ggb-Hinweis: CAS-schreibweise um ohne Gleichheitszeichen auszukommen (=0 kann unterbleiben) |
- aus den Koordinatengleichungen sammele ich die (das sind die Koordinaten der Bildvektoren entsprechend der Basis C) in einer Matrix Ao auf
- (i te Zeile Ao * Basisvektor ) und erhalte die Matrixgleichung
- (2) mit
| Mit (2) kann auch matrizengemäß weitergerechnet werden (3) mit (1) | was von rechts nach links gelesen heißt: ein Vektor wird von Basis C nach Basis E überführt, mit A abgebildet und wieder von Basis E nach Basis C konvertiert |