Factorización de números
En este texto a explicar cómo descomponer números enteros para escribirlos en forma de producto de potencias de números primos (forma factorizada).
Ejemplo:
El número 360 se puede escribir como el producto
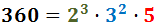 Las bases de las potencias son los números primos 2, 3 y 5.
La factorización de un número como producto potencias de primos es única (el orden de los factores no importa).
Escribir de este modo los números nos servirá, por ejemplo, para simplificar fracciones y encontrar la fracción irreductible equivalentemás rápidamente y para encontrar el mínimo común múltiplo y el máximo común divisor.
Es recomendable conocer las reglas de divisibilidad.
Las bases de las potencias son los números primos 2, 3 y 5.
La factorización de un número como producto potencias de primos es única (el orden de los factores no importa).
Escribir de este modo los números nos servirá, por ejemplo, para simplificar fracciones y encontrar la fracción irreductible equivalentemás rápidamente y para encontrar el mínimo común múltiplo y el máximo común divisor.
Es recomendable conocer las reglas de divisibilidad.
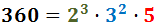 Las bases de las potencias son los números primos 2, 3 y 5.
La factorización de un número como producto potencias de primos es única (el orden de los factores no importa).
Escribir de este modo los números nos servirá, por ejemplo, para simplificar fracciones y encontrar la fracción irreductible equivalentemás rápidamente y para encontrar el mínimo común múltiplo y el máximo común divisor.
Es recomendable conocer las reglas de divisibilidad.
Las bases de las potencias son los números primos 2, 3 y 5.
La factorización de un número como producto potencias de primos es única (el orden de los factores no importa).
Escribir de este modo los números nos servirá, por ejemplo, para simplificar fracciones y encontrar la fracción irreductible equivalentemás rápidamente y para encontrar el mínimo común múltiplo y el máximo común divisor.
Es recomendable conocer las reglas de divisibilidad.La factorización de un número como producto potencias de primos es única (el orden de los factores no importa).
Método
Vamos a explicar el método mientras lo aplicamos para factorizar el número 3780.
1. Representamos una línea vertical y escribimos el número que vamos a descomponer en la parte superior izquierda:
 En el lado derecho escribiremos los divisores (los números por los cuales dividimos); en el izquierdo, los cocientes (resultado de la división del paso anterior).
2. Buscamos un divisor primo del número de la izquierda. Normalmente, empezamos probando por 2, luego por 3, luego por 5, luego por 7...
En nuestro ejemplo, sabemos que 2 es divisor de 3780 porque termina en número par. Escribimos el 2 en la derecha y el resultado de la división 3780/2 lo escribimos en la izquierda, debajo de 3780:
En el lado derecho escribiremos los divisores (los números por los cuales dividimos); en el izquierdo, los cocientes (resultado de la división del paso anterior).
2. Buscamos un divisor primo del número de la izquierda. Normalmente, empezamos probando por 2, luego por 3, luego por 5, luego por 7...
En nuestro ejemplo, sabemos que 2 es divisor de 3780 porque termina en número par. Escribimos el 2 en la derecha y el resultado de la división 3780/2 lo escribimos en la izquierda, debajo de 3780:
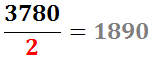
Escribimos los números:
Escribimos los números:
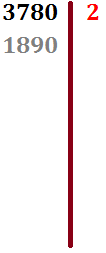
3. Repetimos el proceso, dividiendo entre primos el último número escrito en el lado izquierdo, hasta obtener el cociente 1.
Como 1890 termina en par, es divisible por 2:
3. Repetimos el proceso, dividiendo entre primos el último número escrito en el lado izquierdo, hasta obtener el cociente 1.
Como 1890 termina en par, es divisible por 2:
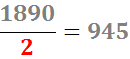
Escribimos los números en la tabla:
Escribimos los números en la tabla:
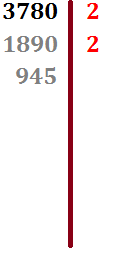
El número 945 no es divisible entre 2 porque termina en número impar. La suma de sus cifras es 18, múltiplo de 3. Por tanto, 945 es divisible por 3:
El número 945 no es divisible entre 2 porque termina en número impar. La suma de sus cifras es 18, múltiplo de 3. Por tanto, 945 es divisible por 3:
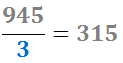 Escribimos en la tabla:
Escribimos en la tabla:
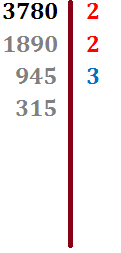 Ya no tenemos que probar si el número es divisible entre 2. Empezamos a buscar a partir de 3:
Ya no tenemos que probar si el número es divisible entre 2. Empezamos a buscar a partir de 3:
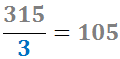
Escribimos los números:
Escribimos los números:
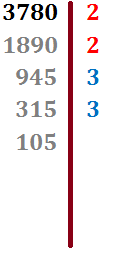
Continuamos con el proceso hasta obtener el cociente 1:
Continuamos con el proceso hasta obtener el cociente 1:
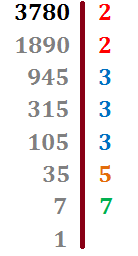
Como ya hemos llegado al 1, el proceso ha terminado.
4. Finalmente, escribimos el número de la parte superior izquierda como un producto de potencias cuyas bases son los divisores y los exponentes son el número de veces que se repite cada divisor:
El 2 se repite dos veces, el 3 se repite tres veces y el 5 y el 7 sólo una vez. Por tanto,
Como ya hemos llegado al 1, el proceso ha terminado.
4. Finalmente, escribimos el número de la parte superior izquierda como un producto de potencias cuyas bases son los divisores y los exponentes son el número de veces que se repite cada divisor:
El 2 se repite dos veces, el 3 se repite tres veces y el 5 y el 7 sólo una vez. Por tanto,

 En el lado derecho escribiremos los divisores (los números por los cuales dividimos); en el izquierdo, los cocientes (resultado de la división del paso anterior).
2. Buscamos un divisor primo del número de la izquierda. Normalmente, empezamos probando por 2, luego por 3, luego por 5, luego por 7...
En nuestro ejemplo, sabemos que 2 es divisor de 3780 porque termina en número par. Escribimos el 2 en la derecha y el resultado de la división 3780/2 lo escribimos en la izquierda, debajo de 3780:
En el lado derecho escribiremos los divisores (los números por los cuales dividimos); en el izquierdo, los cocientes (resultado de la división del paso anterior).
2. Buscamos un divisor primo del número de la izquierda. Normalmente, empezamos probando por 2, luego por 3, luego por 5, luego por 7...
En nuestro ejemplo, sabemos que 2 es divisor de 3780 porque termina en número par. Escribimos el 2 en la derecha y el resultado de la división 3780/2 lo escribimos en la izquierda, debajo de 3780:
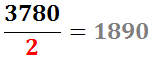
Escribimos los números:
Escribimos los números:
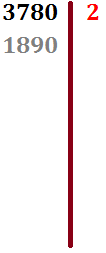
3. Repetimos el proceso, dividiendo entre primos el último número escrito en el lado izquierdo, hasta obtener el cociente 1.
Como 1890 termina en par, es divisible por 2:
3. Repetimos el proceso, dividiendo entre primos el último número escrito en el lado izquierdo, hasta obtener el cociente 1.
Como 1890 termina en par, es divisible por 2:
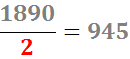
Escribimos los números en la tabla:
Escribimos los números en la tabla:
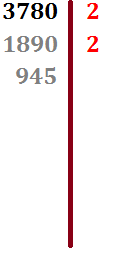
El número 945 no es divisible entre 2 porque termina en número impar. La suma de sus cifras es 18, múltiplo de 3. Por tanto, 945 es divisible por 3:
El número 945 no es divisible entre 2 porque termina en número impar. La suma de sus cifras es 18, múltiplo de 3. Por tanto, 945 es divisible por 3:
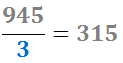 Escribimos en la tabla:
Escribimos en la tabla:
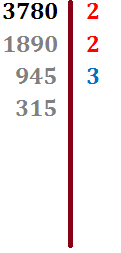 Ya no tenemos que probar si el número es divisible entre 2. Empezamos a buscar a partir de 3:
Ya no tenemos que probar si el número es divisible entre 2. Empezamos a buscar a partir de 3:
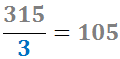
Escribimos los números:
Escribimos los números:

Continuamos con el proceso hasta obtener el cociente 1:
Continuamos con el proceso hasta obtener el cociente 1:

Como ya hemos llegado al 1, el proceso ha terminado.
4. Finalmente, escribimos el número de la parte superior izquierda como un producto de potencias cuyas bases son los divisores y los exponentes son el número de veces que se repite cada divisor:
El 2 se repite dos veces, el 3 se repite tres veces y el 5 y el 7 sólo una vez. Por tanto,
Como ya hemos llegado al 1, el proceso ha terminado.
4. Finalmente, escribimos el número de la parte superior izquierda como un producto de potencias cuyas bases son los divisores y los exponentes son el número de veces que se repite cada divisor:
El 2 se repite dos veces, el 3 se repite tres veces y el 5 y el 7 sólo una vez. Por tanto,
