Euklids bevis for vinkelsummen i en trekant
Elementerne bog I sætning 32
Trin 1
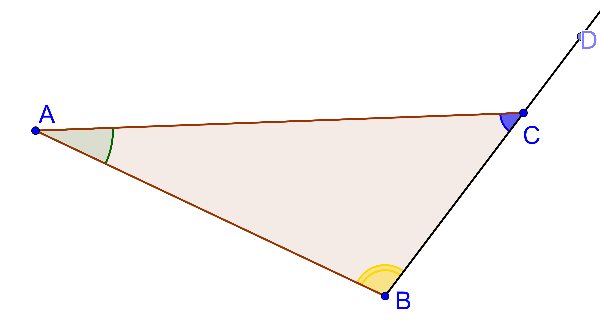
Trin 2
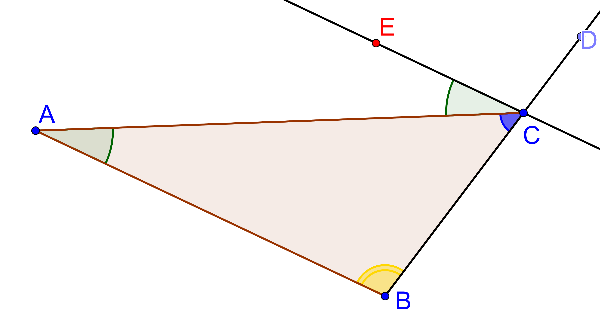
Spm 1: Supplementvinklen DCE
Liniestykket CE er konstrueret parallelt til liniestykket AB (side i trekant ABC). Vinklen DCB er lige (to rette, ), fordi konstruktionen var, at BC blev forlænget til D. I ovenstående billede (Trin 2): Hvilke vinkler deler supplementvinklen DCA i figuren Trin 2?
Spm 2: Vinkelpar (vekselvinkler)
I billedet ovenfor (trin 2), hvilke to vinkler hører sammen som vekselvinkler, som brugt i Euklid i første bog, sætning 28 i konstruktionen, hvor en ret linie falder på to parallelle (rette) linier?
Trin 3
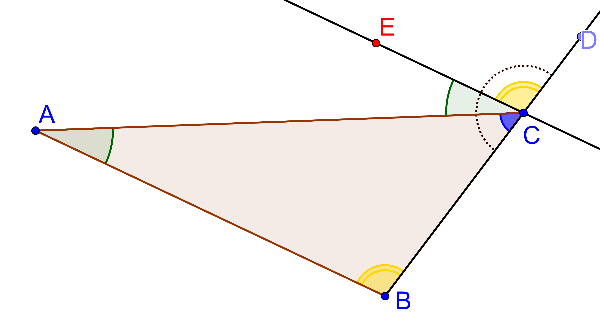
Spm 3: Begrundelse for kongruens (identitet)
De to vinkler CBA og DCE er markeret med den samme signatur for at indikere kongruens, en relation, der beskrives med operatoren . Kongruente vinkler er lige store, identiske, ens. Hvilke egenskaber ved konstruktionen udnytter Euklid til at fastslå, at , altså at de to vinkler er lige store?
Afslutning på beviset
Spm 4: En lige vinkel
Hvor mange grader er en vinkel, når den kaldes lige?