Funzioni lineari a tratti
UNA PREMESSA: FACCIAMO IL PUNTO SUGLI STRUMENTI
Per lavorare in questa pagina avrai bisogno di costruire funzioni, ed in particolari funzioni definite a tratti. A questo scopo Geogebra mette a disposizione due istruzioni:
- VERSIONE 1: Se(Condizione, Allora)
- VERSIONE 2: Se(Condizione, Allora, Altrimenti)
Condizione: quando è vera restituisce AlloraCondizioney = Se(-2<x<3, 4+2x)
otteniamo una funzione che SE x è compresa tra -2 e 3 restituisce 4+2x, altrimenti non è definita - la funzione non esiste fuori da questo intervallo. In termini matematici equivale ad una funzione definita a tratti... con un solo tratto!
La funzione è riprodotta nell'animazione qui sotto.
La funzione f è la retta indicata, ma solo tra -2 e 3: fuori da questo intervallo la funzione non è definita e quindi non restituisce alcun valore. Puoi fare doppio clic sulla definizione della funzione per vedere come è fatto il comando che l'ha generata
la seconda versione di questo comando ci permette di costruire situazioni più articolate: se
potremmo provare a scrivere
Vedi il risultato qui sotto
Condizione è vera restituisce Allora, quando invece Condizione è falsa il risultato è Altrimenti. Ad esempio se dobbiamo riprodurre la funzione definita a tratti
y=se(x<2, x+3, 5-x)Per ottenere risultati ancora più articolati è possibile innestare una dentro l'altra più funzioni del secondo tipo. Ad esempio per ottenere
Possiamo utilizzare una combinazione del tipo
La viene calcolata in questo modo: se (primo intervallo), verrà utilizzata l'espressione altrimenti fa un ulteriore controllo: se è vera (secondo intervallo) calcoleremo la tramite l'espressione , altrimenti (terzo intervallo) useremo la formula .
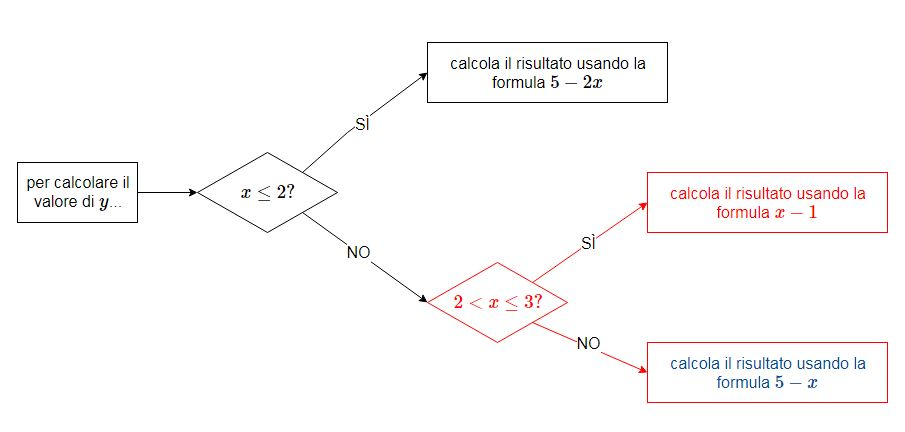
Quando si utilizza una tecnica di questo tipo è importante controllare che le funzioni siano innestate correttamente: ogni nuovo Se svolge il ruolo dell'Altrimenti per il Se precedente; inoltre ogni parentesi che viene aperta deve essere chiusa nel punto opportuno.
Qui sotto vedi la funzione; come al solito puoi cliccare sulla sua espressione per verificare come è fatta.
Si può innestare un numero qualsiasi di controlli uno dentro l'altro, ottenendo così funzioni costituite da un qualsiasi numero di tratti.
Per vedere alcuni esempi di funzioni costruite in questo modo fa riferimento all'applet qui sotto, che puoi cliccare ed ispezionare a piacere. Per visualizzare/nascondere le funzioni clicca sul cerchietto accanto alla loro rappresentazione analitica.