Efecto dominó
Esta actividad pertenece al libro de GeoGebra El dominio del Tiempo.
Esta animación simula el efecto dominó en tiempo real. El efecto dominó se comporta como una onda. La ficha que va en cabeza (el frente de onda) transmite el movimiento de caída a la siguiente, que se convierte así en el nuevo frente de onda.

Cada ficha de este dominó ideal cae siguiendo un movimiento pendular, es decir, su parte superior traza un arco de circunferencia con un movimiento acelerado por la gravedad. Este comportamiento ideal supone las siguientes condiciones:
- Cada ficha no puede desplazarse respecto al suelo, solo puede volcar hasta tropezar con la siguiente. (En la realidad, se producen ligeros desplazamientos.)
- Los choques son completamente inelásticos (no hay rebotes). (En la realidad, se producen pequeños rebotes.)
- Después de golpear la siguiente ficha, la ficha que ha golpeado se desliza sin fricción sobre la otra. (En la realidad, se producen rozamientos y desequilibrios.)
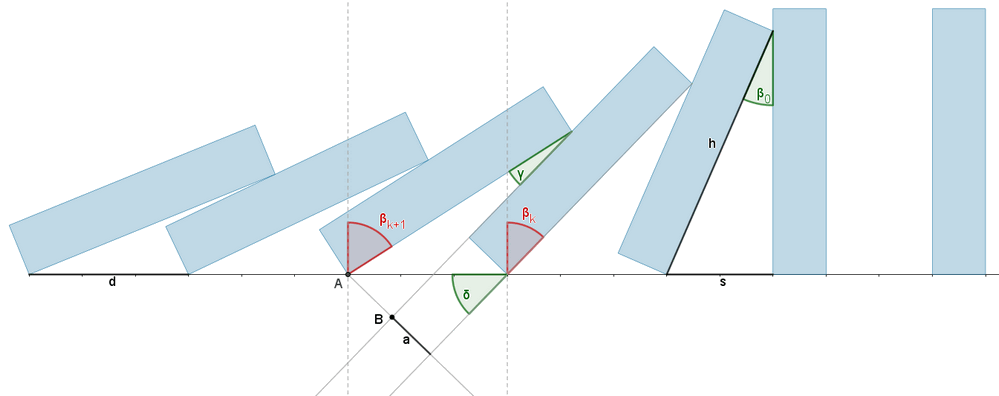
Despejando AB:
y de ahí:
Por lo tanto, la inclinación de cada ficha queda determinada por el ángulo (Mang en la construcción) de la que marcha en cabeza. A su vez, este ángulo de la ficha que arrastra al resto tiene como tope (Mtrans en la construcción):
pues a partir de ahí es la siguiente ficha la que marcha en cabeza (el ángulo de la ficha golpeada pasa de ser 0 a ser , la que golpea pasa de ser a ser , etc.)
Ahora basta definir la función:
para que el comando ListaIteración construya la lista de los ángulos ... :
ListaIteración(f(x), Mang, n)
Para mejorar la ejecución, se recomienda descargar el archivo GGB.
GUION DEL DESLIZADOR anima
# Calcula los segundos dt transcurridos; para ello, suma un segundo si t1(1) < tt
Valor(tt, t1(1))
Valor(t1, Primero(TomaTiempo(), 3))
Valor(dt, (t1(1) < tt) + (t1(1) - tt)/1000)
# Mueve M y controla el final. El valor lógico "trans" registra el momento de colisión con la siguiente ficha
Valor(M, M + dt v)
Valor(trans, Mang > Mtrans ∧ N < n)
Valor(v, Si(trans, (x(vt), 0), vt + dt gt))
Valor(M, Si(trans, Rota((0, h), -Mtrans), M))
Valor(N, Si(trans, N + 1, N))
Valor(M, Si(trans, (0, h) + dt vt, M))
IniciaAnimación(anima, Mang < angMax || N < n)
Autor de la actividad y construcción GeoGebra: Rafael Losada.