Example on max/min functions
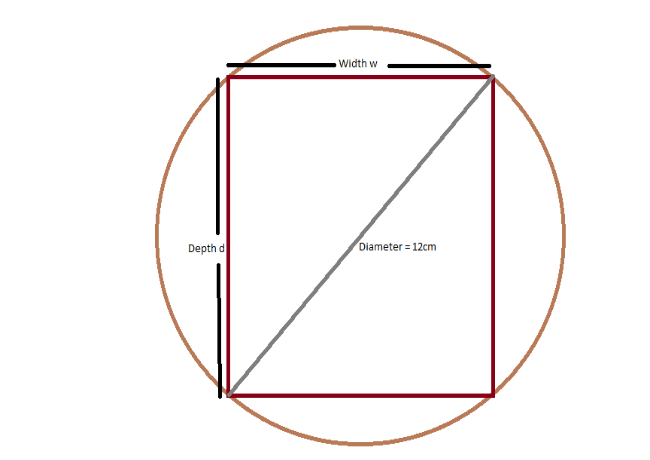
The strenght of a wooden beam is given by , where depends on the type of wood(it is a constant). What is the strongest beam that can be cut from a log with diameter 12cm?
The function provided by the exercise has two variables, but to apply our
Calculus methods, we need to transform it into a function of a single
variable. Knowing the beam will have a rectangular base, we can use
Pythagoras' theorem to find as a function of .
.
Substituting the value in S we get , and its derivative
With a single variable function, the next step is to find the maximum values of the function on the interval , i.e. the critical points on that interval. The graph below shows in green and its derivative in orange, use it to find the maximum of the function on (use an approximation if necessary).
Using the value of the critical point, adjust the sliders in the graph below and compare the value of the area found by min/maxing the problem and other values of and .
Is it possible to find other values for and , on that interval, that creates a stronger beam?