Matemática e a Arte de Navegação Náutica
Introdução
Os nossos antepassados partiram por mar à procura de novas terras, deram novos mundos ao mundo na voz do poeta Luís de Camões.
Tu, também, és um marinheiro de reconhecido valor e afamado entre a marinhagem. Contudo, com o auxílio da Matemática, serás ainda melhor na arte de marinharia.
Considera a seguinte situação:
Devido a este problema, estás perdido no mar, mas consegues avistar dois pontos que estão indicados na tua carta náutica: o rochedo e a boia. Além disso, do ponto em que o teu barco se encontra, consegues medir um ângulo de 60° entre o rochedo e a boia.
Com estas informações, qual é a localização do teu barco na carta náutica?
Considerando R a localização do rochedo, A a localização do teu barco e B a localização da boia, segue as instruções seguintes para te ajudar a encontrar a resposta.
Instruções:
1. Usa a ferramenta  , marca um ponto A na carta náutica;
2. Usando a ferramenta
, marca um ponto A na carta náutica;
2. Usando a ferramenta 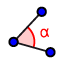 , mede a amplitude do ângulo RAB, selecionando os pontos R, A e B, por esta ordem;
3. Seleciona a ferramenta
, mede a amplitude do ângulo RAB, selecionando os pontos R, A e B, por esta ordem;
3. Seleciona a ferramenta  e move o ponto A, de forma a encontrares uma localização possível para o teu barco.
e move o ponto A, de forma a encontrares uma localização possível para o teu barco.
 , marca um ponto A na carta náutica;
2. Usando a ferramenta
, marca um ponto A na carta náutica;
2. Usando a ferramenta  , mede a amplitude do ângulo RAB, selecionando os pontos R, A e B, por esta ordem;
3. Seleciona a ferramenta
, mede a amplitude do ângulo RAB, selecionando os pontos R, A e B, por esta ordem;
3. Seleciona a ferramenta  e move o ponto A, de forma a encontrares uma localização possível para o teu barco.
e move o ponto A, de forma a encontrares uma localização possível para o teu barco.O ponto que encontraste é a única localização possível para o teu barco?
Como pudeste verificar, o ponto A, a localização do teu barco, existe e não é único.
Efetivamente, o lugar geométrico dos pontos que veem um dado segmento de reta num determinado ângulo é um par de arcos capazes.
A localização do teu barco é um ponto que se encontra sobre um arco capaz de um ângulo inscrito de 60º.
Recorda:
Definição de ângulo inscrito numa circunferência
Dada uma circunferência, dá-se o nome de ângulo inscrito num arco de circunferência a qualquer ângulo que tenha o vértice sobre esse arco e os lados a passarem nos seus extremos.
Definição de arco capaz do ângulo inscrito numa circunferência
Designa-se por arco capaz do ângulo inscrito o arco a que pertence o vértice desse ângulo.
Um pouco de história da Matemática...
O desenvolvimento da Matemática, durante a época áurea da Grécia antiga, foi auxiliado por três importantes ferramentas: a régua não graduada, o compasso e a inteligência humana. A versatilidade desses instrumentos permitiu que a sua utilização se estendesse desde os filósofos gregos até à atualidade com aplicações muito diversificadas no nosso dia a dia, de entre elas, a arte de bem governar uma embarcação.
Agora, vais aprender a construir um arco capaz de um ângulo inscrito numa circunferência, utilizando a régua não graduada e o compasso, como os nossos antepassados.
Com o auxílio de régua não graduada e compasso, simulados através das ferramentas do GeoGebra, vais aprender a construir o arco capaz de um ângulo de 60º de amplitude. Para isso, considera os pontos A e B, já marcados na folha gráfica, e segue as instruções abaixo.
Instruções:
1. Usando a ferramenta 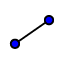 , desenha o segmento de reta AB.
2. Constrói o ângulo BAC com 60º de amplitude. Para tal:
Seleciona a ferramenta
, desenha o segmento de reta AB.
2. Constrói o ângulo BAC com 60º de amplitude. Para tal:
Seleciona a ferramenta 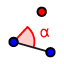 ;
Clica no ponto A e, em seguida, no segmento de reta AB (escreve 60º e escolhe a opção "sentido anti-horário");
Clica com o botão direito do rato sobre o ponto B', escolhe a opção "Renomear" e escreve C;
Desenha o segmento de reta AC.
3. Traça a mediatriz do segmento de reta AB. Para tal, seleciona a ferramenta
;
Clica no ponto A e, em seguida, no segmento de reta AB (escreve 60º e escolhe a opção "sentido anti-horário");
Clica com o botão direito do rato sobre o ponto B', escolhe a opção "Renomear" e escreve C;
Desenha o segmento de reta AC.
3. Traça a mediatriz do segmento de reta AB. Para tal, seleciona a ferramenta 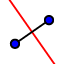 e clica sobre [AB].
4. Traça a reta perpendicular a [AC] e que passa no ponto A. Para tal, seleciona a ferramenta
e clica sobre [AB].
4. Traça a reta perpendicular a [AC] e que passa no ponto A. Para tal, seleciona a ferramenta 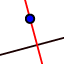 clica quer sobre [AC] quer sobre o ponto A.
5. Determina o ponto de interseção da mediatriz do segmento de reta AB (etapa 3) com a reta perpendicular a [AC] e que passa no ponto A (etapa 4). Para tal, seleciona a ferramenta
clica quer sobre [AC] quer sobre o ponto A.
5. Determina o ponto de interseção da mediatriz do segmento de reta AB (etapa 3) com a reta perpendicular a [AC] e que passa no ponto A (etapa 4). Para tal, seleciona a ferramenta  , clica numa reta e, depois, na outra. Surge o ponto D (centro da circunferência que passa pelos pontos A e B). De seguida, renomeia o ponto D para O.
6. Desenha o arco de circunferência de centro no ponto O e extremos nos pontos A e B. Para tal, seleciona a ferramenta
, clica numa reta e, depois, na outra. Surge o ponto D (centro da circunferência que passa pelos pontos A e B). De seguida, renomeia o ponto D para O.
6. Desenha o arco de circunferência de centro no ponto O e extremos nos pontos A e B. Para tal, seleciona a ferramenta 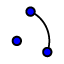 e clica sobre os pontos O, A e B, por esta ordem.
7. Constrói um ponto P sobre o arco de circunferência que desenhaste na etapa anterior. Para isso, seleciona a ferramenta
e clica sobre os pontos O, A e B, por esta ordem.
7. Constrói um ponto P sobre o arco de circunferência que desenhaste na etapa anterior. Para isso, seleciona a ferramenta 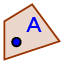 e clica sobre o referido arco. De seguida, renomeia o ponto D para P.
8. Constrói os segmentos de reta PA e PB.
Agora, podes observar o ângulo BPA inscrito na circunferência de centro O e raio [OA].
9. Mede a amplitude do ângulo BPA. Para tal, seleciona a ferramenta
e clica sobre o referido arco. De seguida, renomeia o ponto D para P.
8. Constrói os segmentos de reta PA e PB.
Agora, podes observar o ângulo BPA inscrito na circunferência de centro O e raio [OA].
9. Mede a amplitude do ângulo BPA. Para tal, seleciona a ferramenta 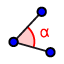 , clica no segmento de reta PB e, em seguida, no segmento de reta PA.
10. Selecionando a ferramenta
, clica no segmento de reta PB e, em seguida, no segmento de reta PA.
10. Selecionando a ferramenta  , move o ponto P e observa a medida de amplitude do ângulo BPA.
, move o ponto P e observa a medida de amplitude do ângulo BPA.
 , desenha o segmento de reta AB.
2. Constrói o ângulo BAC com 60º de amplitude. Para tal:
Seleciona a ferramenta
, desenha o segmento de reta AB.
2. Constrói o ângulo BAC com 60º de amplitude. Para tal:
Seleciona a ferramenta  ;
Clica no ponto A e, em seguida, no segmento de reta AB (escreve 60º e escolhe a opção "sentido anti-horário");
Clica com o botão direito do rato sobre o ponto B', escolhe a opção "Renomear" e escreve C;
Desenha o segmento de reta AC.
3. Traça a mediatriz do segmento de reta AB. Para tal, seleciona a ferramenta
;
Clica no ponto A e, em seguida, no segmento de reta AB (escreve 60º e escolhe a opção "sentido anti-horário");
Clica com o botão direito do rato sobre o ponto B', escolhe a opção "Renomear" e escreve C;
Desenha o segmento de reta AC.
3. Traça a mediatriz do segmento de reta AB. Para tal, seleciona a ferramenta  e clica sobre [AB].
4. Traça a reta perpendicular a [AC] e que passa no ponto A. Para tal, seleciona a ferramenta
e clica sobre [AB].
4. Traça a reta perpendicular a [AC] e que passa no ponto A. Para tal, seleciona a ferramenta  clica quer sobre [AC] quer sobre o ponto A.
5. Determina o ponto de interseção da mediatriz do segmento de reta AB (etapa 3) com a reta perpendicular a [AC] e que passa no ponto A (etapa 4). Para tal, seleciona a ferramenta
clica quer sobre [AC] quer sobre o ponto A.
5. Determina o ponto de interseção da mediatriz do segmento de reta AB (etapa 3) com a reta perpendicular a [AC] e que passa no ponto A (etapa 4). Para tal, seleciona a ferramenta  , clica numa reta e, depois, na outra. Surge o ponto D (centro da circunferência que passa pelos pontos A e B). De seguida, renomeia o ponto D para O.
6. Desenha o arco de circunferência de centro no ponto O e extremos nos pontos A e B. Para tal, seleciona a ferramenta
, clica numa reta e, depois, na outra. Surge o ponto D (centro da circunferência que passa pelos pontos A e B). De seguida, renomeia o ponto D para O.
6. Desenha o arco de circunferência de centro no ponto O e extremos nos pontos A e B. Para tal, seleciona a ferramenta  e clica sobre os pontos O, A e B, por esta ordem.
7. Constrói um ponto P sobre o arco de circunferência que desenhaste na etapa anterior. Para isso, seleciona a ferramenta
e clica sobre os pontos O, A e B, por esta ordem.
7. Constrói um ponto P sobre o arco de circunferência que desenhaste na etapa anterior. Para isso, seleciona a ferramenta  e clica sobre o referido arco. De seguida, renomeia o ponto D para P.
8. Constrói os segmentos de reta PA e PB.
Agora, podes observar o ângulo BPA inscrito na circunferência de centro O e raio [OA].
9. Mede a amplitude do ângulo BPA. Para tal, seleciona a ferramenta
e clica sobre o referido arco. De seguida, renomeia o ponto D para P.
8. Constrói os segmentos de reta PA e PB.
Agora, podes observar o ângulo BPA inscrito na circunferência de centro O e raio [OA].
9. Mede a amplitude do ângulo BPA. Para tal, seleciona a ferramenta  , clica no segmento de reta PB e, em seguida, no segmento de reta PA.
10. Selecionando a ferramenta
, clica no segmento de reta PB e, em seguida, no segmento de reta PA.
10. Selecionando a ferramenta  , move o ponto P e observa a medida de amplitude do ângulo BPA.
, move o ponto P e observa a medida de amplitude do ângulo BPA.
O que podes concluir ao moveres o ponto P, ao longo do arco de circunferência, relativamente à medida de amplitude do ângulo BPA?
Voltando ao problema... O vento ficou bonançoso e o mar amainou. Por isso, agora, vês não só o rochedo e a boia como também o farol 01 (indicados na tua carta náutica). No ponto em que o teu barco se encontra, para além de conseguires medir um ângulo de 60º entre o rochedo e a boia, consegues medir um ângulo de 70º entre o farol 01 e o rochedo. Com esta nova informação, já consegues encontrar a localização exata do teu barco na carta náutica?
Para poderes confirmar a tua resposta anterior, explora a seguinte apliqueta do GeoGebra, seguindo as instruções.
Instruções:
1. Seleciona as caixas de verificação "arco capaz de 60º" e "arco capaz de 70º";
2. Move os arcos capazes que surgem para encontrares a localização do teu barco;
3. Determina a interseção dos dois arcos capazes;
4. Assinala a localização do teu barco com o ponto A;
5. Verifica que o teu ponto A cumpre as condições do enunciado do problema.
Créditos
Atividade adaptada do recurso experimento "Arco Capaz e Navegação", da autoria de Leonardo Barichello, da coleção de recursos "Recursos educacionais multimídia para a matemática do ensino médio" da M3 em parceria com a Unicamp.
Ligação para o recurso desta atividade na rede
https://m3.ime.unicamp.br/recursos/996
Este trabalho está licenciado sob CC BY-NC-SA 4.0
