Outline
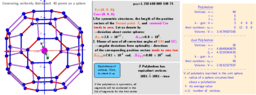
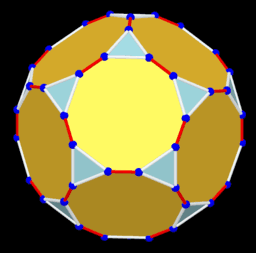
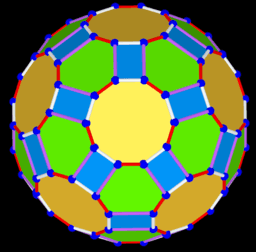
₈Polyhedra with extreme distribution of equivalent vertices
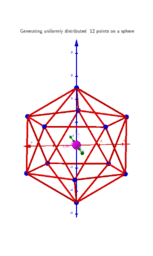
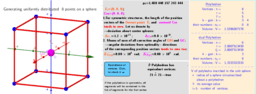
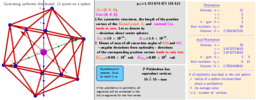
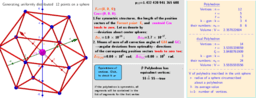
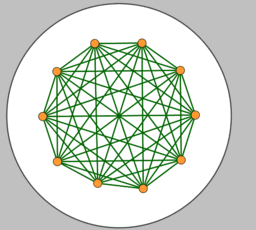
For a given number of n particles on a sphere, we consider only polyhedrons whose vertices, firstly, are extremely distributed and, secondly, equivalent to each other.
By extreme distributions, we mean the distribution of points on the sphere that correspond to the local extrema (maxima) of Distance Sum. The sum of distances is measured by summing all the segments connecting each possible combination of 2 points. The "measure" of this distribution is the average distance between particles on the unit sphere(pn). The method of Lagrange multipliers is used to find the extreme distributions of particles on a sphere.
*From Book: Extended definitions of point location estimates https://www.geogebra.org/m/hhmfbvde
From: List of My Public Books on GeoGebra Topics: Constructing polyhedra -https://www.geogebra.org/m/eabstecp