Oefening 4 p 102


Werkmethode:
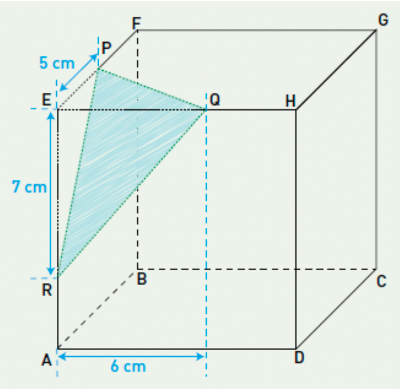
- Om de lijnstukken te tekenen met de gevraagde lengtes werden 2 cirkels getekend die gelegen zijn in het vlak (A,E,F) telkens met middelpunt E en respectievelijk als straal 6 en 7 (zo verkrijg je de punten Q en R) en één bol (zo verkrijg je het punt P).
Deze irrationale resultaten zijn natuurlijk onmiddellijk duidelijk door Pythagoras toe te passen in de verschillende driehoeken.
We tekenen de driehoek op ware grootte.
Werkmethode:
- Klik op de driehoek en toon het aanzicht gekeken vanuit die driehoek.
Volume van de piramide die je bekomt in a is:
Om een gelijkzijdige driehoek te krijgen met zijde 6 moet er voldaan zijn aan:
= met x de afstand tot het hoekpunt.
Dus is x =
Werkmethode:
- Teken een bol met middelpunt E en met een straal van
- Duid de snijpunten met de ribben aan en teken de driehoek.
- Het is een gelijkzijdige driehoek.
Een sterk moment!

Bereken het volume van de hierboven afgesnede piramide en de hoogte van deze piramide.
Om |RI| te berekenen, kan je de sinusregel toepassen in driehoek RPI.
Nadien kan je dan de hoogte van de piramide berekenen:
Dus: h =
De oppervlakte van PQR is makkelijk te berekenen:
OPP PQR =
Het volume van de piramide is dan:
Inhoud piramide =
